En nuestro día a día estamos rodeados de números e información: cuántos libros leemos en un mes, las notas que sacamos en una asignatura o las edades de los alumnos en clase. Para entender mejor todos esos datos, en matemáticas usamos tres conceptos muy útiles: la media, la mediana y la moda.
Estos tres se aprenden en Educación Primaria y forman parte de la estadística, una rama de las matemáticas que nos ayuda a analizar y comparar información. La media nos dice cuál es el promedio, la mediana muestra el valor que está en el centro, y la moda nos indica cuál es el dato que más se repite.
En otros post anteriores hemos hablado de las medidas y datos en matemáticas. Ahora es momento de conocer bien qué significa cada uno de estos conceptos. Veremos la diferencia entre media y mediana, cómo se calculan paso a paso y para qué sirven. Y al final, podrás practicar con unos ejercicios fáciles sobre la media, la mediana y la moda.
Índice
Diferencia entre media y mediana
A veces, cuando tenemos muchos datos necesitamos resumirlos con un solo número que nos diga algo importante. Para eso usamos media y mediana, pero no son lo mismo.
La media es lo que muchos llaman el «promedio»: se suman todos los números y se divide entre cuántos hay. En cambio, la mediana es el número que está justo en el centro cuando ordenamos todos los datos de menor a mayor. Ambas son formas de resumir los datos, pero la manera de calcularlas y el tipo de información que nos dan es diferente.
Imagina que tienes las siguientes notas: 5, 6, 7, 10 y 10.
- La media sería (5 + 6 + 7 + 10 + 10) ÷ 5 = 7,6
- La mediana es 7, el número que está justo en medio.
Entonces, ¿cuál usar?
- La media es útil cuando los datos son parecidos entre sí y no hay ningún número que se aleje mucho del resto. Por ejemplo, imagina que cinco alumnos sacaron estas notas: 7, 8, 8, 9 y 8. La media es (7 + 8 + 8 + 9 + 8) ÷ 5 = 8. Como todos sacaron notas parecidas, la media representa muy bien al grupo. En este caso, la media y mediana suelen estar cerca y dan una idea clara del rendimiento.
- La mediana va mejor cuando hay un número que se sale mucho del resto (lo que se llama un “valor extremo”). Por ejemplo, si alguien sacó un 1 o un 10 y el resto de notas son medias. En esos casos, la media puede dar un resultado que no representa bien al grupo. Por ejemplo, imagina que cinco alumnos sacaron estas notas: 3, 4, 5, 6, 10. La media sería (3 + 4 + 5 + 6 + 10) ÷ 5 = 5,6. La mediana es 5, que es el número del medio. Aquí vemos cómo la media y mediana pueden dar resultados diferentes, y por eso es importante saber cuál conviene más usar. Por eso, cuando hay un dato muy alto o muy bajo que cambia todo, es mejor usar la mediana.
Saber distinguir entre media y mediana nos ayuda a interpretar mejor los datos en situaciones reales. Ambas formas son buenas, pero dependiendo del caso, una puede mostrar mejor lo que queremos saber.
Qué es la media
La media es una medida de tendencia central que resume un conjunto de datos mediante un solo valor representativo, obtenido mediante algún tipo de promedio. En otras palabras, la media es una forma de representar «el valor típico» de un conjunto de datos, y existen diferentes tipos de medias según el contexto o la naturaleza de los datos.
Medias en estadística
En estadística, usamos diferentes tipos de medias dependiendo del tipo de datos que tenemos. La más común es la media aritmética, pero también existen otras como la media ponderada o la media geométrica, que se usan en cursos más avanzados.
- Media aritmética: la más común. Se calcula sumando todos los números y dividiendo entre cuántos hay.
- Media ponderada: cuando unas cosas valen más que otras. A veces, no todo cuenta igual. Por ejemplo, en el caso de que para evaluar una asignatura un examen valga más que una tarea, usamos la media ponderada:
- Examen: 9 (vale el doble)
- Tarea: 6
- Entonces para calcular la media ponderada, hacemos: (9 × 2 + 6 × 1) ÷ (2 + 1) = (18 + 6) ÷ 3 = 24 ÷ 3 = 8. La media ponderada es 8, ¡más alta que si hiciéramos el promedio normal!
- Media geométrica: se usa cuando hay porcentajes o crecimientos. En vez de sumar, se multiplican los números y se saca una raíz. Por ejemplo, si tu dinero crece un 20% un año y un 10% el siguiente:
- Eso es como tener 1,20 y luego 1,10.
- Multiplicas: 1,20 × 1,10 = 1,32
- Sacas la raíz cuadrada: √1,32 ≈ 1,15
Media aritmética
La media aritmética es el resultado de sumar todos los valores de un conjunto de datos y dividir el total entre la cantidad de valores. Es el valor que tendrían todos los datos si fueran todos iguales.
Cómo se calcula la media aritmética
Calcular la media es muy sencillo. Solo tienes que:
- Sumar todos los números del conjunto de datos.
- Dividir el total entre la cantidad de números que hay.
Fórmula de la media aritmética
La fórmula que usamos en matemáticas para encontrar la media es:
Por ejemplo, si tienes estas edades: 10, 11, 12
Qué es la mediana
La mediana es el número que está justo en el centro cuando ordenamos un conjunto de datos de menor a mayor. Es muy útil porque nos muestra el valor que divide los datos en dos partes iguales: la mitad de los números son menores y la otra mitad son mayores.
No hay un símbolo único como en otras operaciones, pero a veces verás la mediana representada con Med(X) o Mediana(X). También puede escribirse simplemente como “Mdn”.
A diferencia de la media, la mediana no se ve afectada por valores muy grandes o muy pequeños, lo que la hace ideal para representar los datos cuando hay un número que se sale mucho del resto. Por eso, entender bien la diferencia entre media y mediana es clave para elegir la más adecuada en cada situación.
Cómo se calcula la mediana
-
Ordena todos los números de menor a mayor.
-
Si la cantidad de números es impar, la mediana es el número del centro. Ejemplo:
- Números: 4, 6, 2, 9, 3
- Ordenados: 2, 3, 4, 6, 9
- La mediana es 4 (es el dato del centro)
- Si es par, se suman los dos del centro y se dividen entre dos. Ejemplo:
- Números: 5, 2, 8, 6
- Ordenados: 2, 5, 6, 8
- Hay dos en el centro: 5 y 6
- La mediana es 5,5.
Fórmula mediana
No hay una sola fórmula como la media, pero se puede expresar así:
-
Si hay un número impar de datos:
-
Si hay un número par de datos:
¿Qué es la moda?
Después de conocer bien la media y mediana, es momento de descubrir otro concepto importante en estadística: la moda. La media y mediana nos ayudan a entender el promedio o el punto central de los datos, pero la moda nos dice cuál es el valor que más se repite. Aunque no siempre se habla tanto de ella, la moda también es muy útil para analizar datos del día a día.
No tiene nada que ver con la ropa ni con las tendencias, aunque la idea es parecida: es el número que está “de moda” porque aparece más veces que los demás.
¿Cómo se calcula la moda?
Es muy fácil:
-
Mira todos los números del grupo.
-
Cuenta cuántas veces aparece cada uno.
-
El que más se repite es la moda.
Por ejemplo, imagina que estás contando los juguetes favoritos de tus amigos: Peluche, coche, coche, pelota, coche, muñeca. El juguete que más veces aparece es coche (3 veces), así que la moda es “coche”.
Seguro que en algún momento te has preguntado ¿cómo saber que estás a la moda? , espero que con la definición que hemos visto o la explicación de cómo calcular la moda sepas encontrar la respuesta a esta pregunta.
Media, mediana y moda: ejemplo
Imagínate que preguntamos a todos nuestros compañeros de clase qué nota han sacado en matemáticas este trimestre. Como somos 25, obtenemos 25 datos:
7, 4, 6, 8, 3, 9, 5, 6, 4, 6, 7, 10, 2, 7, 5, 6, 8, 5, 9, 3, 5, 5, 5, 3, 2
Un poco complicado de entender algo, ¿verdad? ¿Qué sería lo primero que harías con estos datos? Yo lo primero que haría sería ordenarlos.
2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8, 8, 9, 9, 9, 10
Ahora ya vemos algunas cosas: tengo muchos compañeros entre el 5 y el 6
2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8, 8, 9, 9, 9, 10
y sólo han suspendido 7.
2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8, 8, 9, 9, 9, 10
Pero podemos hacernos muchas más preguntas sobre estos datos que tenemos. La primera que se suele hacer es ¿se puede decir que mi clase saca, en general, buenas notas en mates o no? ¿Cómo decidimos esto? Con la media de las notas de la clase.
-
- Contamos cuántos datos tenemos. En nuestro caso, 25.
- Sumamos los datos: 2 + 2 + 3 + 3 + 3 + 4 + 4 + 4 + 5 + 5 + 5 + 5 + 5 + 5 + 6 + 6 + 6 + 6 + 7 + 7 + 7 + 8 + 8 + 9 + 9 + 9 + 10 = 140
- Dividimos el resultado entre el número de datos:
Así que la nota media de la clase es 5,6. Fíjate que esto no quiere decir que en mi clase todos saquemos un 5,6. La media sería 5,6 en casos tan extremos como que todos sacáramos un 5,6 o que 14 alumnos sacaran un 10 y los once restantes un cero… y muchos otros.
En todo caso, cuando hablemos de las notas de mi clase, en lugar de dar toda la lista puedo decir que la nota media es un 5,6. Eso le dará una idea al que me oiga de por dónde va la cosa, y podrá compararla con otras clases donde la nota media sea un 4 o un 8, por decir dos números.
Aunque la media nos ayuda mucho, no siempre es suficiente. A veces necesitamos complementarla con la mediana para tener una visión más clara. Por eso es tan importante conocer bien la media y mediana.
Vamos a imaginarnos ahora que llega un compañero nuevo. No sabemos qué nota va a sacar, ¿qué crees que pasará con la media?
-
-
- Si saca un 0, la media quedará en:
- Si saca un 5, la media quedará en:
- Y si saca un 10:
- Si saca un 0, la media quedará en:
-
Fíjate en que si saca un 5, que está cerca de la media que teníamos antes, ¡la media casi no cambia! Pero si saca un 0 o un 10, que están muy lejos de la media, entonces cambia ¡dos décimas! Entonces la media cambia mucho cuando llega un nuevo dato que se aleja mucho de ella. Para evitarlo, podemos usar la mediana.
Para arreglar el problema anterior, vamos a ver cómo se halla la mediana.
Lo primero que hay que hacer (si no lo hemos hecho ya) es poner los datos en orden.
2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8, 8, 9, 9, 9, 10
Y ahora buscamos el dato que está en el medio:
2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8, 8, 9, 9, 9, 10
¡Esa es la mediana! Cuando usamos tanto la media y mediana, tenemos más herramientas para analizar datos y entender lo que realmente está pasando.
Ahora vamos a hallar la mediana en los tres casos. Como ahora tenemos 26 datos y no hay ninguno en el medio, hacemos la media de los dos que estén en el centro. Si nuestro nuevo compañero:
-
-
- Saca un 0:
-
0, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8, 8, 9, 9, 9, 10
-
-
- Saca un 5:
-
2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8, 8, 9, 9, 9, 10
-
-
- Saca un 10:
-
2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8, 8, 9, 9, 9, 10, 10
Como ves, la mediana solo ha cambiado cuando saca un 10. Realmente es solo una coincidencia porque en general, la mediana no cambia mucho con datos alejados de la media… ¡pero en general no quiere decir siempre!
Ahora, vamos a ver la moda, recordemos que es el número que más veces se repite en un conjunto de datos. Vamos a contar cuántas veces aparece cada número en tu lista:
-
-
-
2 → 2 veces
-
3 → 3 veces
-
4 → 3 veces
-
5 → 6 veces ✅
-
6 → 4 veces
-
7 → 3 veces
-
8 → 2 veces
-
9 → 3 veces
-
10 → 1 vez
-
-
La moda es 5, porque es el número que más se repite (6 veces).
Ejercicios media, mediana y moda
Ahora que ya conoces qué son la media y mediana, además de la moda, es momento de poner en práctica lo aprendido. A través de estos ejercicios sencillos y divertidos de Smartick, podrás reforzar tus conocimientos y entender mejor cómo se usan estas tres formas de analizar datos.
Ejercicio 1
Respuesta:
La media de venta es de 5 libros por semana.
Ejercicio 2 media
Respuesta:
La media es 3 dibujos diarios.
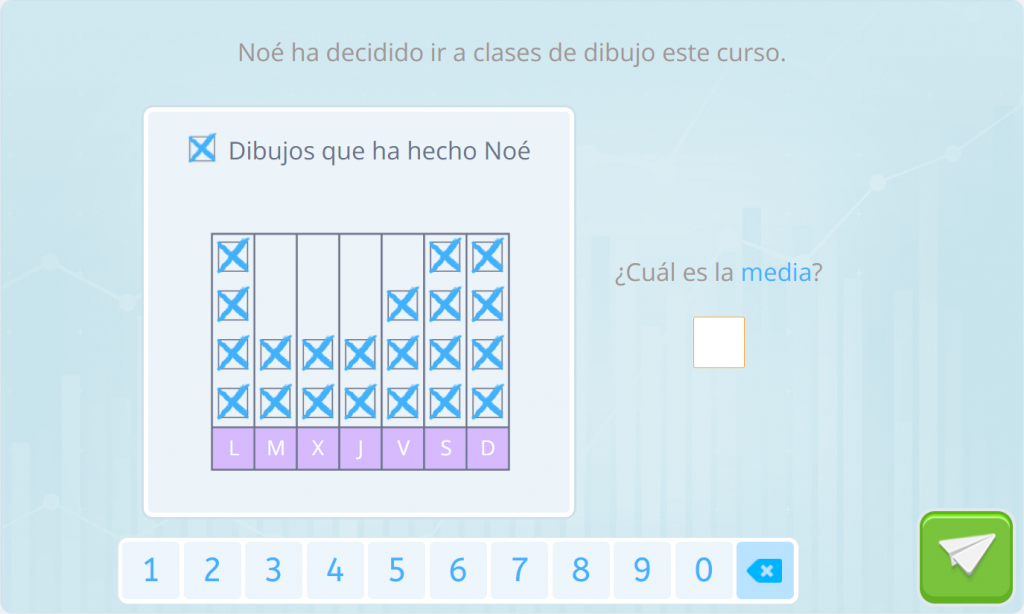
Ejercicio 3 media
Respuesta:
La media es de 40 litros de agua.
Ejercicio mediana
Respuesta:
5 – 5 – 6 – 6 – 7 – 7 – 8 – 8 – 9
La mediana es 7 porque una vez ordenados los datos de menor a mayor, queda la misma cantidad de números a amabos lados del 7.
Ejercicio moda
Respuesta:
-
-
- Galleta → 7 veces ✅
- Bombón → 6 veces
- Helado → 3 veces
-
La moda es «Galleta».
Ahora que ya sabes qué son la media y mediana, junto con la moda, y cómo se calculan, podrás entender mejor los datos en muchas situaciones cotidianas. Estos conceptos te ayudan a interpretar notas, edades o cualquier conjunto de números de forma clara. ¿Te ha sido útil este post acerca de la media y mediana y la moda? Compártelo en tus redes sociales y prueba Smartick gratis.
Para seguir aprendiendo:
- ¿Cómo saber que estás a la moda?
- Factorizar en números primos
- Valor absoluto de un número
- Números primos y números compuestos
- Estrategia de suma: números consecutivos
- Figuras geométricas. Clasificación, tipos y ejemplos - 20/03/2017
- Nuevos contenidos de Smartick - 11/07/2016
- Ejercicios de lógica en Smartick II - 23/06/2016

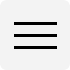









Buen material, pero me gustaría hacer una apreciación importante.
Me parece un gran error interpretar que la media de 5,6 quiere decir «en general, las notas de mi clase rondan el 5.6».
Esta es una mala interpretación de lo que significa una media.
Piénsese que en esa muestra de 25 alumnos, si hay 14 que saquen un 10 y 11 que saquen un cero también sale de media 5,6.
Muchas gracias Andrés por tu comentario que nos ayuda a mejorar el blog de Smartick. Ya hemos revisado la frase para que el concepto de media quede más claro.
hola siempre que le suelen dejar tareas a mi hija reviso su pagina y así me ayudo a recordar mis tiempos de colegio, gracias me es de mucha ayuda. =).
Muchas gracias me sirvió mucho para explicarle a mi nieto.
¡Gracias por tu comentario, María! Te invito a que visites nuestra página web y pruebes el método Smartick con tu nieto. Con 15 minutos al día de ejercicios podrá aprender cálculo, geometría, lógica, programación, comprensión lectora ¡y mucho más! todo ello mientras trabaja de forma individual y personalizada, realizando sesiones adaptadas a su nivel. ¡Entra y pruébalo gratis!
https://www.smartick.es
¡Un saludo!
Muy claro, gracias.
gracias, soy profesora de primaria y me ayudó a encontrar una forma fácil de enseñar a mis niños. Dios la bendiga. ¡Éxitos!
Gracias, no lo había entendido pero contigo ya sé sobre la media y la mediana, te lo agradezco.